Free PLTL algebras and a coalgebraic extension of hyperdoctrines
This blog post provides an overview of the work I had done with José Siqueira this summer. Inspired by the free Boolean/Heyting algebra of a given set, we develop a free-forgetful adjunction between posets and PLTL temporal algebras, where PLTL denotes propositional linear temporal logic. We provide a description of their induced Eilenberg-Moore categories. We describe how this could be used to temporalise systems and logics through hyperdoctrines and connect this to the stream comonad. We end with future research directions, connecting this topic with the cofree comonad of polynomial functors and temporalising doxastic logic.
1 Introduction
Time was. Time is. Time will be.
Time is a concept embedded in our reality. Yet, when we consider the truth of statements, the logics we conceive might not have temporal aspects. Whether in propositional logic, predicate logic or epistemic logic, once a statement holds, it holds forever, no matter the time or the place.
But there are times and places when and where this is not true. Though the statement “it is raining” might not be true now, it might be true the next day. And if you are outside tomorrow, soaking in the rain, the statement “Rain is hitting you” might only hold until you arrive home.
Though many logics do not have the ability to describe these time-dependent statements, a family of modal logics do, known as temporal logics. There are many types of temporal logic: interval temporal logic (see Della Monica et al. 2011; also Moszkowski 2012), Lamport’s temporal logic of actions (see Lamport 1994; also Rabinovich 1998), computation tree logic (see Reynolds 2001), and other possibilities. Each temporal logic is grounded in a specific (philosophical) interpretation of time, contains differing modalities for time, and has numerous applications beyond mathematics and philosophy, such as in the formal verification of computational systems.
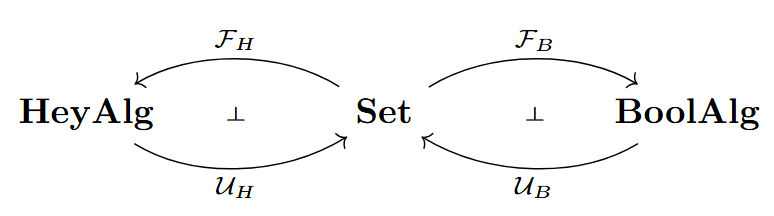
As with any logic, a natural question arises: is there a corresponding algebra to it? This question comes from mathematical logic, whereby given a logical theory T, one asks whether one can construct the Lindenbaum-Tarski algebra A induced by T. When T consists of propositional tautologies and the logic is classical, one finds that the Lindenbaum-Tarski algebra is the Boolean algebra. Likewise, if T is the theory of intuitionistic logic, then the Lindenbaum-Tarski algebra is the Heyting algebra. We therefore ask: for which temporal logics can we apply Tarski’s method1 and develop temporal algebras?
In this post, we’ll be focusing on a form of temporal logic called propositional linear temporal logic (PLTL), with the hopes of upgrading statements (that is, predicates) on interfaces that use classical logic into statements on systems that are time-dependent. To do this, we will work through four key parts:
We describe the axioms and rules of PLTL. From this, we can develop its theory.
We develop the category of PLTL algebras, describe the free PLTL algebra of a poset (such as a Boolean or Heyting algebra), and consider the PLTL algebras induced by a monad from this free-forgetful adjunction.
We tie this into José Siqueira’s recent work (see Siqueira 2025) on hyperdoctrines (which describe underlying logics such as classical or intuitionistic propositional logic), and how to temporalise them using PLTL.
We give the example of the stream comonad, which describes \omega-sequences, and how to temporalise statements about these sequences.
2 PLTL
Let us introduce PLTL, as described in Reynolds (2001).
2.1 Axioms and Rules of PLTL
Suppose we have a countable set of atomic propositions, denoted \mathcal{L}. We can then consider all the well-formed formulae constructed from \mathcal{L} using \top, \neg, \land (assuming a classical logic), which achieves the propositional part of PLTL.
Suppose we wish to consider how the truth value of propositions may change over time. How should we interpret time?
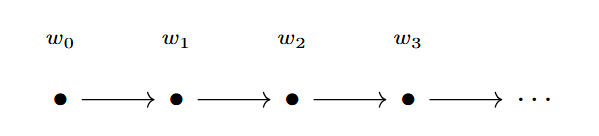
One way to view time is as a linear timeline in countably many discrete steps, starting from the present and heading to the future. We observe this as a \omega-sequence w of time instants w_i for i \in \mathbb{N}, where w_0 marks the present moment.
At each time instant w_i, we evaluate whether a proposition is true or not at that instant. We also consider how the future looks from w_i: this leads to defining the notation w_{\geq i} = \langle w_i, w_{i+1}, w_{i+2}, \dots \rangle, which is simply the linear timeline w starting from time instant w_i. Thus, we formally view w_i as the subset of well-formed PLTL formulae which are true at that time instant.
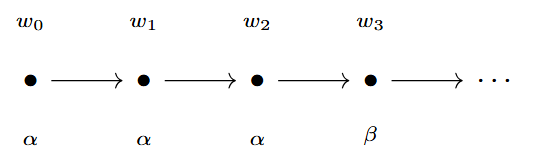
We introduce two temporal connectives alongside the two classical connectives \neg and \land: X, a unary operator denoting the neXt time instant, and U, a binary operator where \alpha U \beta denotes \alpha holding \beta, from which we can recursively build well-formed formulae of PLTL from \top and the atomic propositions in \mathcal{L}.
The truth of a PLTL formula is evaluated at these \omega-sequences. We define w \vDash \alpha if and only if the formula \alpha is true of the sequence w by recursion:
- w \vDash \top,
- w \vDash p if and only if p \in w_0, for any atomic p \in \mathcal{L},
- w \vDash \neg \alpha if and only if w \not \vDash \alpha,
- w \vDash \alpha \land \beta if and only if w \vDash \alpha and w \vDash \beta,
- w \vDash X\alpha if and only if w_{\geq 1} \vDash \alpha,
- w \vDash \alpha U \beta if and only if there is some i \geq 0 such that w_{\geq i} \vDash \beta and for each 0 \leq j < i, w_{\geq j} \vDash \alpha.
We then define satisfiablity and logical validity, \vDash_{PL} \alpha, as usual. We also define two derived temporal connectives: F \alpha = \top U \alpha for a future operator and G \alpha = \neg F \neg \alpha for a guarantee/global operator.
There is also, of course, a syntactic side to this story2; what we just described is a sound and complete semantics for the associated notion of proof (Reynolds (2001)). We use this deductive system to define a notion of derivability \vdash_{PL} in the usual manner.
2.2 Free-Forgetful Adjunctions of Algebras and (Po)Sets
Let us observe the following adjunctions and the fact that Boolean algebras and Heyting algebras may be seen as the respective algebras for classical and intuitionistic logic:
One may ask for an analogy with PLTL. To this aim, we must answer what a PLTL algebra is, what the morphisms between PLTL algebras are, and what the free construction of a PLTL algebra looks like on a poset. This will allow us to consider PLTL algebras as a category, which we can use to temporalise statements later!
2.2.1 What is a PLTL Algebra?
We fix a signature \Sigma_{PL} with constants \bot, \top, unary operators \neg, X, and binary operators \land, U. We can then define a theory T_P for PLTL as consisting of a bounded distributive lattice with complements with imposed inequalities corresponding to our axiom schema for PLTL3.
With this theory T_P, we can then define the category of PLTL algebras, \textbf{PLTL-Alg}, as the category with:
- Objects as tuples A = (|A|, \leq_A; \bot^A, \top^A, \neg^A, X^A, \land^A, U^A), where |A| is a set, (|A|, \leq_A) is a poset, and the operators of A (including the derived operators F^A and G^A) satisfy the axioms of T_{PL}, and
- Morphisms as monotone homomorphisms h: A \rightarrow B preserving all the symbols, including the derived classical and temporal connectives.
It is worth noting a free-forgetful adjunction between \textbf{BoolAlg} and \textbf{PLTL-Alg}, but we relegate this as an interesting observation.
2.2.2 What is the free PLTL algebra of a poset?
Given a poset (P, \leq_1), we may view inequalities p \leq_1 q as axioms stemming from P, and so encode the order of P by setting \text{Th}_P \coloneqq \{p \rightarrow^P q : p \leq_1 q \}.
To construct the free PLTL algebra of P, we perform the Lindenbaum-Tarski method. We first recursively build a set F(P) as follows:
- P \subseteq F(P),
- \phi \land^P \psi, \phi U^P \psi \in F(P) for \phi, \psi \in F(P),
- \bot^P, \top^P \in F(P), and
- \neg^P \phi, X^P\phi \in F(P) for \phi \in F(P).
We can then define a new theory T_{P} \coloneqq T_{PL} \cup \text{Th}_P, which can be seen as the theory of PLTL combined with the imposed theory from the poset P.
We can also define an equivalence relation4 on F(P) via \phi \sim_{T_P} \psi if and only if T_P \vdash \phi \leftrightarrow^P \psi (that is, if \phi and \psi are equivalent in the theory of T_P).
We thus obtain the Lindenbaum-Tarski algebra of T_P, denoted by \mathcal{F}_{PL}(P) \coloneqq F(P)/\sim_{T_P}. We can also define an ordering \leq_2 on \mathcal{F}_{PL}(P) via [\phi] \leq_2 [\psi] if and only if T_{P} \vdash \phi \rightarrow^P \psi. This makes (\mathcal{F}_{PL}(P), \leq_2) into a poset, and in fact a PLTL-Algebra.
Intuitively, this poset is simply all the well-formed PLTL formulae from a beginning poset of propositions P (think classical or intuitionistic propositional logic), quotiented by logical equivalence.
2.3 The Eilenberg-Moore Category of PLTL Algebras
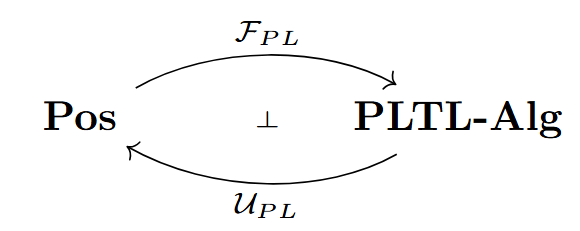
Of course5, this construction \mathcal{F}_{PL}:\textbf{Pos} \rightarrow \textbf{PLTL-Alg} is functorial, and we may observe the following free-forgetful adjunction:
From this adjunction, we obtain a monad (M, \eta^M, \mu^M), where: * M \coloneq \mathcal{U}_{PL}\mathcal{F}_{PL} sends a poset P to a poset corresponding to the free PLTL algebra of P; * \eta^M is the unit that sends p to [p]; and, * \mu^M is the multiplication that maps a formula-of-formulae to a formula.
It is worth explaining \mu^M further with some examples. First, observe that elements of M^2(P) are equivalence classes of PLTL formulae, generated by elements of M(P), which are themselves equivalence classes [\phi] of PLTL formulae over P. Examples include:
- [([X\phi] \land [\psi]) U [X\chi]]
- [[\alpha] \lor [G\beta] \lor [\gamma]]
- [G([\varPhi] U [G\varPsi]) \rightarrow \neg X [\varXi]].
Intuitively, \mu^M collapses a formula-of-formulae into a formula by interpreting each inner equivalence class [\varphi] as any element of [\varphi], such as \varphi, in M(P), then evaluating the formula as an equivalence class. For example, with the first example above:
- The constants are [X \phi], [\psi], [X\chi] \in M(P).
- Applying \mu_P^M, we map each inner equivalence class [\varphi] to an element of [\varphi], such as \varphi. Thus, [X \phi] \mapsto X\phi, [\psi] \mapsto \psi, [X\chi] \mapsto X\chi.
- Then, we evaluate this as an equivalence class, so:
\mu_P^M\big([([X\phi] \land [\psi]) U [X\chi]]\big) = [(X\phi \land \psi) U (X\chi)] \in M(P).
Similarly, \mu_P^M\big([[\alpha] \lor [G\beta] \lor [\gamma]]\big) = [\alpha \lor G\beta \lor \gamma] and \mu_P^M\big([G([\varPhi] U [G\varPsi]) \rightarrow \neg X [\varXi]]\big) = [G(\varPhi U (G \varPsi)) \rightarrow \neg X\varXi].
That this works is because the equivalence class of a formula-of-formulae in M^2(P) does not depend on the choice of representatives of the inner equivalence classes.
As with any free-forgetful adjunction, we may now consider the Eilenberg-Moore category \textbf{Pos}^M induced by this monad (M, \eta^M, \mu^M), whose objects are M-algebras (P, v^P:MP \rightarrow P).
One may understand an object (P, v^P) of \textbf{Pos}^M as a poset equipped with an interpretation map, where the generators of MP (so the elements of P) are interpretated as themselves and a consistent interpretation is chosen for formulae, subject to the requirement that evaluating these formulae respects substitution.
One can then prove an equivalence between \textbf{PLTL-Alg} and \textbf{Pos}^M, thus showing a PLTL algebra is practically the same as an M-algebra.
2.4 Hyperdoctrines and Temporalisation
Here is how everything relates to José’s work (see Siqueira 2025)!
Suppose the following set-up:
- I is a comonad on \mathcal{C}, so I^{\text{op}} is a monad on \mathcal{C}^{\text{op}},
- L is a monad on \textbf{Pos}, which represents a modality acting on \textbf{Pos} such as M, and
- P:\mathcal{C}^\text{op} \rightarrow \textbf{Pos} is a hyperdoctrine. That is, a functor to \textbf{Pos} that encodes a flavour of logic, such as classical or intuitionistic propositional logic.
In his recent work, José Siqueira proved that (regular) hyperdoctrines are the same as symmetric monoidal double functors \mathbf{\mathbb{S}pan}(\mathcal{C})^{\text{op}} \rightarrow \mathbb{Q}\mathbf{t}(\textbf{Pos}) with a companion commuter property. Further, we know that the 2-category \textbf{Dbl}^{\text{ps}} admits the construction of algebras; i.e, the inclusion \iota: \textbf{Dbl}^{\text{ps}} \hookrightarrow \text{Mnd}(\textbf{Dbl}^{\text{ps}}) has a right adjoint \textbf{$\mathbb{A}$lg}(-) :\text{Mnd}(\textbf{Dbl}^{\text{ps}}) \rightarrow \textbf{Dbl}^{\text{ps}} where \text{Mnd}(\textbf{Dbl}^{\text{ps}}) is the 2-category whose:
- objects are monads in the 2-category \textbf{Dbl}^{\text{ps}}, i.e monads on double categories with respect to pseudo double functors and tight transformations;
- 1-cells are lax morphisms of such monads;
- 2-cells are 2-morphisms of monads.
Now, if I preserves pullbacks, then I^{\text{op}} induces a monad on the double category of spans over \mathcal{C} via the span construction: I^\bullet:\mathbb{S}\textbf{pan}(\mathcal{C})^{\text{op}} \hookrightarrow \mathbb{S}\textbf{pan}(\mathcal{C})^{\text{op}}.
Similarly, we get an induced monad L^\bullet:\mathbf{\mathbb{Q}t}(\textbf{Pos}) \rightarrow \mathbf{\mathbb{Q}t}(\textbf{Pos}) in \textbf{Dbl}^{\text{ps}}. Then, we get a pseudo double functor \textbf{$\mathbb{A}$lg}(I^\bullet) \rightarrow \textbf{$\mathbb{A}$lg}(L^\bullet) whenever we have a map of monads from I^{op} to L by the 2-functoriality of \mathbb{A}lg(-).
It is also known that \mathbb{S}\textbf{pan}(\text{Coalg}(I))^{\text{op}} \simeq \mathbb{A}\textbf{lg}(I^\bullet). Therefore, a map of monads P from I^{\text{op}} on \mathcal{C}^{\text{op}} to L on \textbf{Pos} induces a symmetric monoidal double functor from \mathbb{S}\mathbf{pan}(\mathcal{C})^{\text{op}} to \mathbb{Q}\mathbf{t}(\textbf{Pos}), which is the same as an existential hyperdoctrine. This therefore allows us to consider coalgebras of I as contexts for a hyperdoctrine with semantics in L-algebras.
With this result in mind, let us apply this to our situation, in which \mathcal{C} = \textbf{Set}, P = \text{Sub} is the functor that sends an object to its collection of subobjects in \mathcal{C} and a morphism f:a \to b in \mathcal{C} to f^{-1}:\text{Sub}(B) \to \text{Sub}(A), and L is the monad M induced by the free-forgetful adjunction between \textbf{Pos} and \textbf{PLTL-Alg}, with unit \eta^M and multiplication \mu^M as before.
The key intuition is to view the comonad I on \mathcal{C} as providing an interface, so that P provides a notion of a predicate on this interface. With the result described before, we may then upgrade this predicate to a temporal predicate on systems.
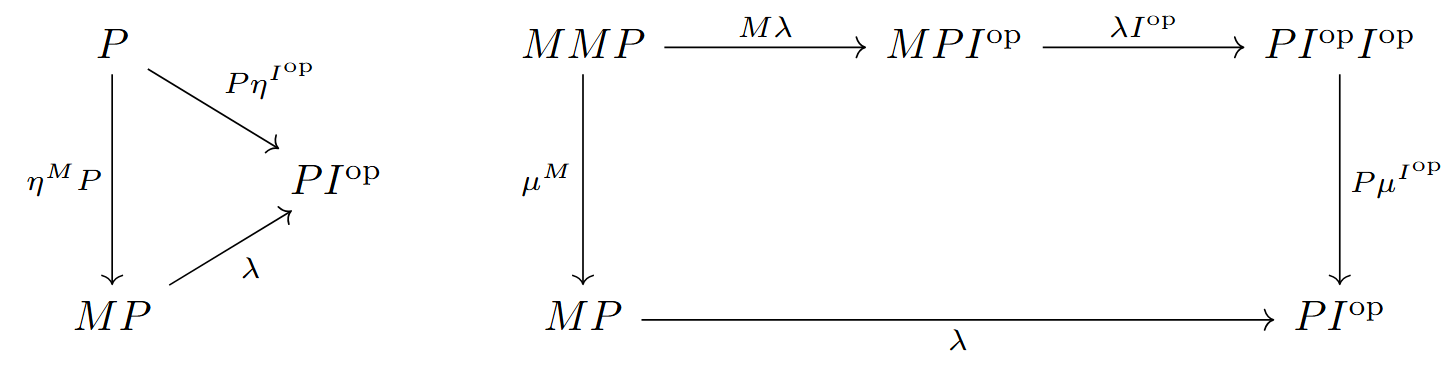
Thus, we ask for which 6 comonads I (so interfaces) we can upgrade, given our P which provides a notion of predicate (in classical propositional logic). That is, for which I is such that there exists a natural transformation \lambda: MP \rightarrow PI^{\text{op}} such that the following diagrams commute:
For us, important examples may come from considering the cofree comonad on various polynomial functors, denoted p as defined in Libkind and Spivak (2024). Let us consider such an example below.
2.4.1 The Stream Comonad
Consider the polynomial functor p(X) = X, which is the identity functor. The cofree comonad of X is the stream comonad I, where I(A) = A^\mathbb{N}, \varepsilon_A(\alpha) = \alpha(0), and \delta_A(\alpha) = (\alpha^{(k)})_{k \in \mathbb{N}}, where \alpha^{(k)}(n) = \alpha(n+k) for \alpha \in A^\mathbb{N}. Then, I^{\text{op}} becomes a monad on \textbf{Set}^{\text{op}} with unit \eta_A^{I^{\text{op}}} = \varepsilon_A^\text{op} and multiplication \mu_A^{I^{\text{op}}} = \delta_{A}^{\text{op}}.
One can then prove that there exists a natural transformation \lambda: MP \rightarrow PI^{\text{op}}, such that (P, \lambda) is a morphism of monads from (\textbf{Set}^{\text{op}}, I^{\text{op}}) to (\textbf{Pos}, M).
It is worth remarking on the proof, and the fact that, to observe \text{Sub}(A^\mathbb{N}) and \text{Sub}((A^\mathbb{N})^\mathbb{N}) as PLTL algebras, one needs to evaluate a given PLTL formula as predicates on A^\mathbb{N} as follows:
- [\top]_A = A^\mathbb{N},
- [\varphi \land \psi]_A = [\varphi]_A \cap [\psi]_A,
- [\varphi U \psi]_A = \{ \alpha: \exists k \geq 0, \alpha^{(k)} \in [\psi]_A \text{ and } \forall 0 \leq j < k, \alpha^{(j)} \in [\varphi]_A \},
- [\neg \varphi]_A = A^\mathbb{N} \backslash [\varphi]_A,
- [X \varphi]_A = \{ \alpha : \alpha^{(1)} \in [\varphi]_A \}.
Here, we interpret each U \subseteq A as predicates about the current stream \alpha^{(0)} = \alpha: that is, we define a current-time predicate \text{cur}^A(U) \coloneqq \{ \alpha \in A^{\mathbb{N}} : \alpha(0) \in U\} \in \text{Sub}(A^\mathbb{N}). Similarly, for a stream-of-streams \Sigma : \mathbb{N} \to A^\mathbb{N}, we may consider each V \subseteq A^\mathbb{N} as predicates regarding the current inner stream, and so define a meta-current-time predicate \text{cur}^{A^\mathbb{N}}(V) \coloneqq \{ \Sigma \in (A^{\mathbb{N}})^\mathbb{N}: \Sigma{(0)} \in V\} \in \text{Sub}((A^\mathbb{N})^\mathbb{N}) and define PLTL operations accordingly. Equivalently, each fibre \text{Sub}(A^\mathbb{N}) is an M-algebra with a corresponding map v^{\text{Sub}(A^\mathbb{N})}: M(\text{Sub}(A^\mathbb{N})) \rightarrow \text{Sub}(A^\mathbb{N}), which also defines each \text{Sub}((A^\mathbb{N})^\mathbb{N}) as an M-algebra.
We may then define the natural transformation \lambda via \lambda_A \coloneqq v^{\text{Sub}(A^\mathbb{N})} \circ M(\text{cur}^A):M(\text{Sub(A)}) \rightarrow \text{Sub}(A^\mathbb{N}).
With (P, \lambda) a map of monads, we then observe the following map, for each set A: \lambda_A: MPA \rightarrow PI^\text{op}A Since M is the monad that produces the free PLTL-algebra of P(A), MPA is the set of all PLTL-formulae generated from A. Likewise, PI^{\text{op}}A is a poset of predicates on the set I^{\text{op}}A = A^\mathbb{N}, and so describes properties of streams, or possible behaviours of a sequence of states.
Then, \lambda_A sends each formula \varphi \in MPA to a predicate \lambda_A(\varphi) \in P(I^\text{op}A). Thus, given a stream \alpha \in A^\mathbb{N}, the predicate \lambda_A(\varphi) determines whether \alpha \vDash_A \varphi. Thus, the behaviour of a PLTL formula is its characteristic predicate on streams, aka: [\varphi]_A \coloneqq \lambda_A(\varphi):A^\mathbb{N} \rightarrow \Omega where \Omega is the truth poset in the hyperdoctrine P.
One may therefore consider MP as providing the syntax, whilst PI^{\text{op}} provides the semantics. Viewing I as an interface that exposes an entire trajectory of states and P as providing predicates on I, the natural transformation \lambda allows us to interpret each temporal formula as the set of streams satisfying it, thus upgrading a predicate on X into a predicate on IX, consistent with PLTL semantics.
Importantly, given our choice of monad L = M, we require a valid interpretation of the PLTL operators X and U in terms of the semantics of the cofree comonad of the polynomial functor on \textbf{Set}^{\text{op}}. This is fairly obvious for the stream comonad, but certainly not obvious for polynomial functors whose cofree comonads exhibit branching behaviour (aka, polynomials of degree 2 or higher).
2.5 Future Directions
From here, there are many natural research directions to explore.
We had provided a category of PLTL algebras, \textbf{PLTL-Alg}, based on constructing the Lindenbaum-Tarski algebra of the theory of propositional linear temporal logic. As stated before, PLTL is one of many possible temporal logics, grounded in a specific philosophical interpretation of time as starting from the present and extending to the future in discrete, countable time steps. There are many other temporal logics of interest, and we ask whether they may undergo a similar treatment to PLTL. Of particular note are the following logics:
- Intuitionistic Linear Temporal Logic, as explored in Balbiani et al. (2019) and Fernández-Duque, McLean, and Zenger (2024), which may allow us to upgrade classical predicates on states to intuitionistic temporal predicates on streams.
- Doxastic Logic, as explored in Rönnedal (2018) or Zhang et al. (2025), which may allow us to hold epistemic predicates on streams as opposed to temporal predicates.
- Computation Tree Logic, as explored in Reynolds (2001), which may allow us to consider predicates on branches of streams, as opposed to only a linear timeline of streams as we currently see with the stream comonad.
With any monad L in our set-up, a natural question is which comonads I allow for the hyperdoctrine P to be a map of mornads, such that this upgrade of predicates is possible. This is particularly interesting when we allow I to be the cofree comonad of polynomial functors p(X).
As described before, it could be the case that, for L = M, the only polynomial functors p for which I allows for such a construction is when p = B \times X for B: that is, for unary polynomials with no constants. Though limiting, it suggests that we ought to consider other logics (such as CTL) which can account for more sophisticated system behaviours (primarily, branching behaviours).
We can also change the hyperdoctrine itself to reflect the underlying logic that we temporalise via PLTL. Primarily, if one develops a hyperdoctrine that accounts for a static form of doxastic logic, then setting L to be a monad induced by a free-forgetful adjunction of temporal algebras (such as PLTL) allows one to consider a dynamic or temporal doxastic logic that can apply to systems. In Dagnino and Rosolini (2021), they show that modal interior operators may be constructed from adjunctions in the 2-category of doctrines. Likewise, one could instead consider a temporal hyperdoctrine , then upgrade it with a doxastic monad. That there may be two ways to approach this might imply two interpretations of a logic affected with temporal and doxastic modalities, the priority of which depends on the set-up. This suggests a potentially novel way to define dynamic doxastic or temporal doxastic logics.
References
Footnotes
Tarski’s method does not apply to every logic, as will be discussed later.↩︎
The rules are modus ponens and temporal generalisation (or the necessitation rule for G): \frac{\alpha, \alpha \rightarrow \beta}{\beta} \hspace{20pt} \frac {\alpha}{G \alpha}. The axioms are substitutional instances of the following: C0, any propositional tautology; C1, F \neg \neg \alpha \leftrightarrow F\alpha; C2, G(\alpha \rightarrow \beta) \rightarrow (G\alpha \rightarrow G\beta); C3, G\alpha \rightarrow (\alpha \land X\alpha \land X(G\alpha)); C4, X \neg \alpha \leftrightarrow \neg X \alpha; C5, X (\alpha \rightarrow \beta) \rightarrow (X\alpha \rightarrow X\beta); C6, G (\alpha \rightarrow X\alpha) \rightarrow (\alpha \rightarrow G\alpha); C7, (\alpha U \beta) \leftrightarrow (\beta \lor (\alpha \land X(\alpha U \beta))); C8, (\alpha U \beta) \rightarrow F \beta.↩︎
With F and G as defined before, we impose the following (in)equalities, corresponding to the PLTL axiom schema: C1, F \neg \neg \alpha = F\alpha; C2, G(\alpha \rightarrow \beta) \leq (G\alpha \rightarrow G\beta); C3, G\alpha \leq (\alpha \land X\alpha \land X(G\alpha)), so paired with temporal generalisation, we get G\alpha = \alpha, G\alpha \leq X\alpha and G\alpha \leq XG\alpha; C4, X \neg \alpha = \neg X \alpha; C5,X (\alpha \rightarrow \beta) \leq (X\alpha \rightarrow X\beta); C6, G (\alpha \rightarrow X\alpha) \leq (\alpha \rightarrow G\alpha); C7, (\alpha U \beta) = (\beta \lor (\alpha \land X(\alpha U \beta))); C8, (\alpha U \beta) \leq F \beta.↩︎
We have an equivalence relation and a partial ordering on \mathcal{F}_{PL}(P) as a consequence of the example given on page 27 of Fred Kröger (2008).↩︎
Read the corresponding paper to this article.↩︎
For arbitrary P, I, and L, this need not be the case. As a counterexample, take \mathcal{C} = \textbf{Set}, P = \mathcal{P} be the powerset functor, I = \text{id}_{\mathcal{C}} be the identity comonad, so I^{\text{op}} is the identity monad, and L be the monad such that L(X) = \mathbf{1} (the terminal object of \textbf{Pos}) for all X \in \textbf{Pos}.↩︎